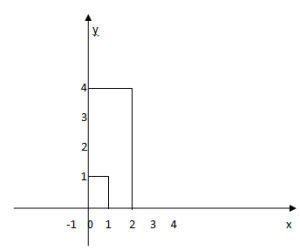
Dengan x dan y disebut sebagai variabel atau peubah, a dan b adalah koefisien dari kedua variabel serta c adalah konstanta. Variabel x dan y harus berpangkat/berorde 1.
GRAFIK PERSAMAAN GARIS LURUS
Persamaan garis lurus dapat digambarkan dalam koordinat cartesius untuk mendapatkan grafik yang berbentuk garis lurus. Berikut ini langkah-langkah untuk menggambar grafik garis tersebut:
- Menentukan dua titik yang dilalui oleh garis dalam persamaan tersebut.
- Kedua titik di plot atau ditempatkan pada koordinat cartesius.
- Menghubungkan kedua titik yang telah diplot tersebut untuk menjadi sebuah garis.
Berikut ini bentuk persamaan garis lurus dalam koordinat cartesius:
PENYELESAIAN GARIS LURUS
Dua persamaan garis lurus dapat disajikan bersamaan disebut sebagai sistem persamaan linear
dua variabel dan memiliki bentuk:
Dengan x dan y disebut sebagai variabel atau peubah. Huruf a, b, d dan e adalah koefisien dari masing-masing variabel serta c dan f adalah konstanta.
Ada dua cara dalam penyelesaian sistem persamaan dua variabel yaitu metode substitusi dan metode eliminasi. Berikut penjelasannya:
Metode Substitusi
Dalam metode substitusi, salah satu variabel dipisahkan dari suatu persamaan. Persamaan dalam bentuk

dirubah sehingga memiliki bentuk eksplisit :
atau,
Kemudian persamaan baru tersebut disubstitusikan ke persamaan kedua misalkan
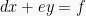
menjadi:
Atau
Persamaan hasil substitusi memiliki 1 variabel sehingga bisa diselesaikan.
Metode Eliminasi
Dalam metode eliminasi, salah satu variabel dieliminasi atau dihilangkan dengan cara pengurangkan kedua persamaan yang ada. Agar variabel bisa dihilangkan saat kedua persamaan dikurangkan, maka koefisien kedua variabel tersebut disamamakan terlebih dahulu. Penyamaan koefisien ini dengan cara mengkali atau membagi suatu persamaan dengan suatu bilangan. Sehingga:
Dengan:
Diperoleh hasil penyelesaiannya:
Nilai variabel y yang telah diketahui dapat disubstitusi kedalam salah satu persamaan untuk mendapat nilai variabel x.
Secara umum ada tiga kasus yang mungkin muncul dalam penyelesaian suatu sistem persamaan ini, yaitu:
Dari gambar disimpulkan:
- Kasus 1, kedua persamaan memiliki satu penyelesaian.
- Kasus 2, kedua persamaan tidak memiliki penyelesaian.
- Kasus 3, kedua persamaan memiliki penyelesaian tak berhingga.
Gradien Persamaan Garis Lurus
Gradien menunjukan kemiringan dari suatu persamaan terhadap garis x. Gradien dinotasikan dengan huruf m. Berdasarkan gambar berikut:
Kemiringan/gradien adalah perbandingan antara jarak garis yang diproyeksikan kesumbu y terhadap proyeksi garis terhadap sumbu x. sehingg
Gradien = m = tan α
Untuk beberapa bentuk persamaan, gradien diperoleh dengan:
Dalam hubungannya suatu persamaan garis lurus dengan garis lainnya, gradien memiliki persamaan sebagai berikut:
Membentuk Persamaan Garis Lurus
1. Jika diketahui gradien dan satu titik yang dilalui
Persamaan garis lurus dapat dibuat dengan mengetahui nilai gradien dan salah satu titik yang dilewati

. Dalam rumus:
Dengan kondisi ini, nilai

dan m telah diketahui. Nilai
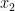
dan

dijadikan variabel x dan y, sehingga rumus gradien nya bisa dimodifikasi menjadi:
Atau:
2. Jika diketahui dua titik yang dilalui
Jika yang diketahui adalah kedua titik

dan
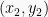
yang dilewati garis dan gradien tidak diketahui rumusnya diperoleh dari modifikasi rumus sebelumnya yaitu:
Menjadi:
Atau:
Contoh Soal Persamaan Garis Lurus dan Pembahasan
Contoh Soal 1
Tentukan persamaan garis A yang memotong sumbu y = 3 dan tegak lurus dengan garis B yang melalui titik pusat O dan titik (3, 2).
Pembahasan:
Diketahui:
- A melalui (0,3)
- B melalui (0,0) dan (3,2)
- A dan B tegak lurus, maka
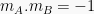
Sehingga:
Selanjutnya:
Contoh Soal 2
Jika suatu garis melewati dua titik yaitu
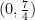
dan
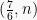
serta sejajar garis 2y + 3x – 6 = 0, maka tentukan nilai n.
Pembahasan:
Garis sejajar dengan 2y + 3x – 6 = 0, maka gradien keduanya sama.
Sehingga:
Contoh Soal 3
Tiga garis A, B, C memiliki gradien masing-masing 3, 4, 5. Ketiga garis memotong sumbu y di titik yang sama. Jika absis masing-masing absis garis ke sumbu x dijumlahkan adalah
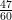
, tentukan persamaan garis A.
Pembahasan:
Diketahui persamaan masing-masing garis:
Karena memotong sumbu y di yang sama, maka
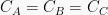 . Selanjutnya disebut C.
. Selanjutnya disebut C.
Absis (saat y=0) masing-masing garis adalah:
Ketiga absis dijumlahkan:
Sehingga:
Dan persamaannya menjadi:
Dapat dieliminasi dengan mengurangi persamaan pertama dengan kedua :